Recently, I saw this codeforce problem https://codeforces.com/problemset/problem/1257/G, so I start to figure out how FFT works.
Iterative FFT
Let \(a\) be the original sequence and \(b\) is the sequence after divide and conquer,
Then we can observe that:
\[b_i = a_{reverse(i)} \iff b_{reverse(i)} = a_i\]Let’s initialize \(j = 0\) index for \(a\) and \(i = 0\) index for \(b\), note that we can accelerate the procedure by incremental and in-place fashion, that is
\[b_{i = 0} = a_{reverse(i) == 0}\]Given the fact that:
\[b_{i + 1} = a_{reverse(i+1)}\], we can actually exploit the previous step \(j == reverse(i)\) result.
Let us rewrite it to: \(reverse(j) == i\), then we can plug \(j\) into the update step.
\[b_{i + 1} = a_{reverse(reverse(j) + 1)}\]Though \(reverse(reverse(j) + 1))\) seems crazy, it can actually be implemented fast by bitwise operations in reverse_add below.
Horay! Let’s see the code
int reverse_add(int x, int bit_length)
{
// try to find the most first bit that is 0
for(int l = 1 << bit_length; (x ^= l) < l; l >>= 1);
return x;
}
void bit_reverse(int n, complex_t *x)
{
int bit_length = (int) log2(n);
for(int i = 0, j = 0; i != n; ++i)
{
if(i > j) swap(x[i], x[j]);
j = reverse_add(j, bit_length);
}
}
Let us try this example:
\[w^{0}_{8}, w^{1}_{8}, w^{2}_{8}, w^{3}_{8}, w^{4}_{8}, w^{5}_{8}, w^{6}_{8}, w^{7}_{8}\]where \(w^{k}_{n} = e^{\frac{2 \pi i k}{n}}\).
And a polynomial ( I use the vector notation introduced by MIT open course):
\[A(x) = a_0 x^0 + a_1 x^1 + a_2 x^2 + .... a_7 x^7 = < a_0, a_1, ..., a_7 >(x)\]Let’s see the computational graph:
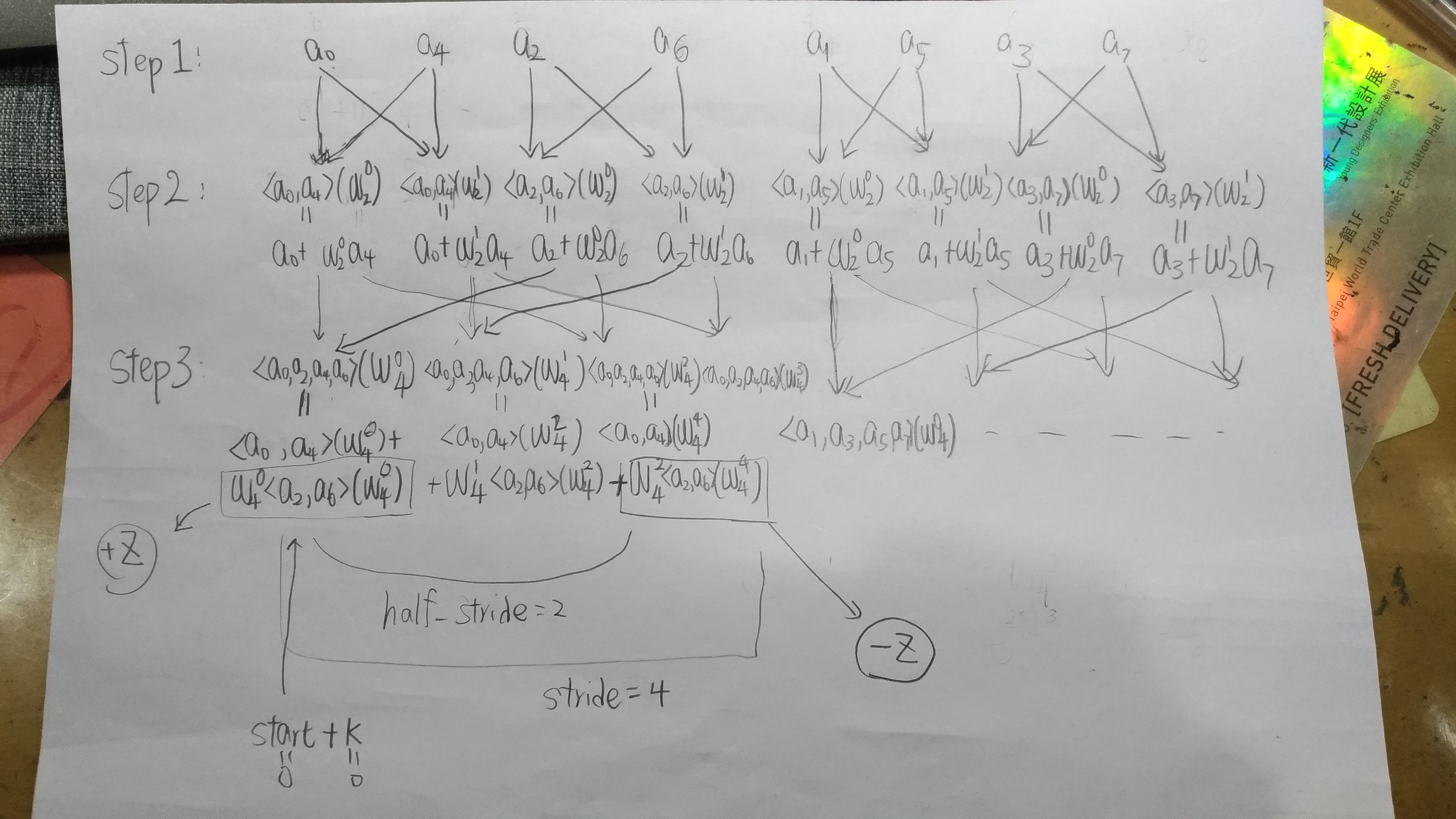
Code:
void transform(int n, complex_t *x, complex_t *w)
{
// Prepare the leaf nodes ( you can see this as a bottom-up approach )
bit_reverse(n, x);
for(int stride = 2; stride <= n; stride <<= 1)
{
int half_stride = stride >> 1;
// the start index of a stride region
for(int start = 0; start < n; start += stride)
{
// this loop will finish up [start, start + stride] region
for(int k = 0; k < half_stride; ++k)
{
complex_t z = x[start + half_stride + k] * w[n / stride * k];
// Use the phase property (see below)
x[start + half_stride + k] = x[start + k] - z;
x[start + k] = x[start + k] + z;
}
}
}
}
Note, in the code,
\[z = ... \cdot w^{k}_{stride} = ... \cdot w^{k * \frac{n}{stride}}_{n}\]and the phase property:
\[w^{k + \frac{n}{2}}_{n} = e^{\frac{2 \pi i}{n} \cdot \frac{n}{2}} \cdot w^{k}_{n} = - w^{k}_{n}\]Recursively FFT
Here is the pseudocode:
fft(<a0, a1, a2, a3 ... , an-1>){
result = [None] * n
even = fft(<a0, a2, ... an-2>) // even[i] == A(w^{i}_{n/2})
assert(len(even) == n/2)
odd = fft(<a1, a3, ..., an-1>)
assert(len(odd) == n/2)
for(int i = 0; i < n; i++){
// A(w^i_n) = A_even(w^{2i}_n) + w^i_n * A_odd(w^{2i}_n)
// See the fact below.
result[i] = even[i % (n/2)] + w^i_n * odd[i % (n/2)]
}
return result
}
This is the code written by miskoo (See reference):
void fft(int n, complex<double>* buffer, int offset, int step, complex<double>* epsilon)
{
if(n == 1) return;
int m = n >> 1;
fft(m, buffer, offset, step << 1, epsilon);
fft(m, buffer, offset + step, step << 1, epsilon);
for(int k = 0; k != m; ++k)
{
int pos = 2 * step * k;
temp[k] = buffer[pos + offset] + epsilon[k * step] * buffer[pos + offset + step];
temp[k + m] = buffer[pos + offset] - epsilon[k * step] * buffer[pos + offset + step];
}
for(int i = 0; i != n; ++i)
buffer[i * step + offset] = temp[i];
}
For some people, this code is hard to understand at the first glance. So let us visualize it!:
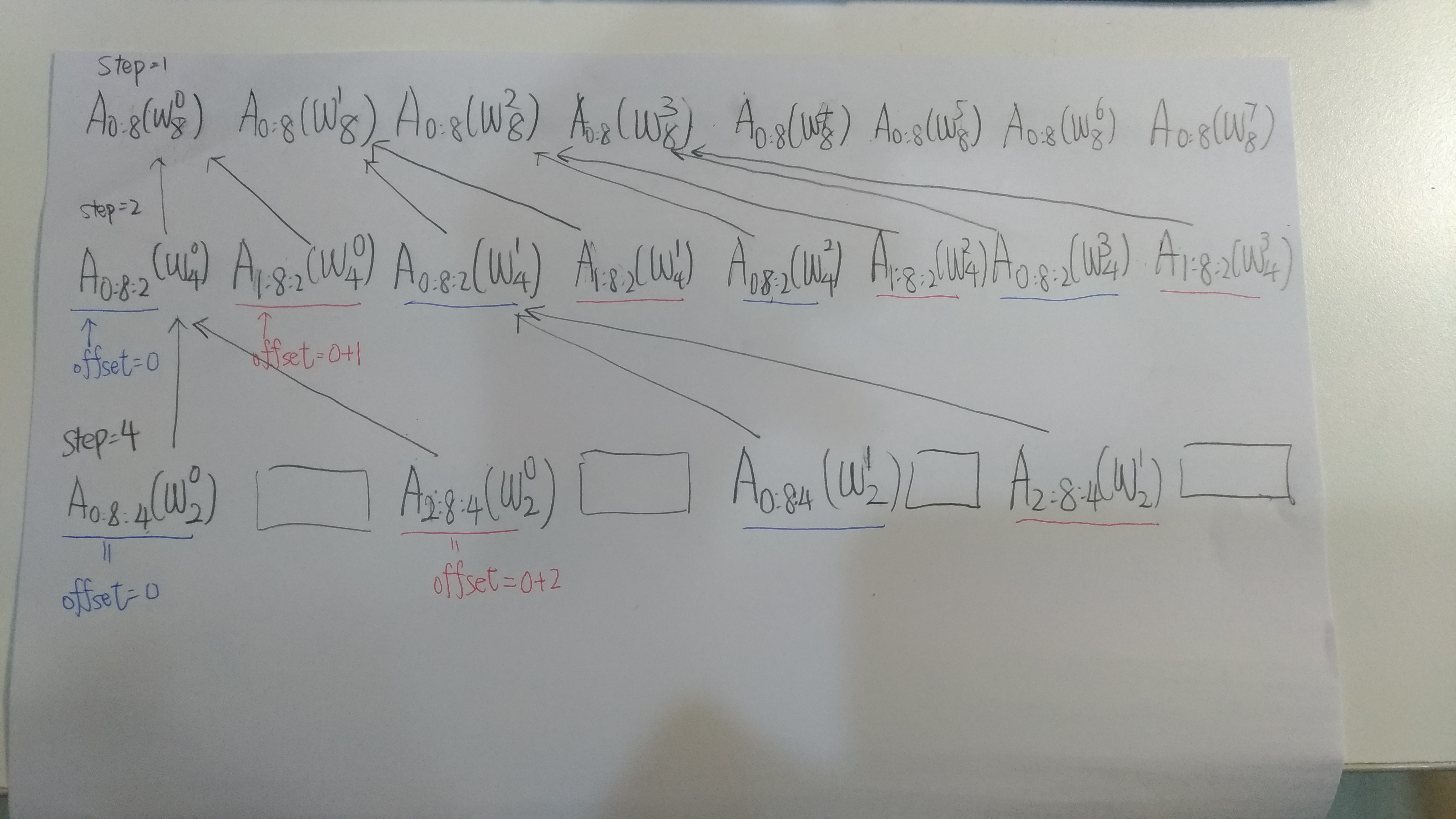
Note that for simplicity, I denote:
\[A_{i:j:step}(x) = <a_i, a_{i+step}, ... >(x) \text{(Not include $j$)}\]Number Theoretic Transform (NTT)
Procedure of NTT
- Let \(n\) (must be the power of 2) be the transformed size of an input vector.
- Choose a prime number \(p\) in the form of \(p = k \cdot n + 1\), where \(k \geq 1\). By Dirichilet prime theorem, you are guaranteed to find a \(k\) such that \(p\) is a prime.
- Let \(g\) be the primitive \(p - 1\) root of unitiy (or say, primitive root modulo \(p\)). (It is guaranteed that you can find a \(g\) by the property of multiplicative group \(\mathbb{Z}_p\), though I don’t know why.) Note that: \(\{ g^0, g^1, g^2, ... g^{p-2} \}\) under modulo \(p\) are unique.
- Define \(w_n \equiv g^k \mod p\). By Euler theorem, \(w^n_n = g^{kn} = g^{p-1} = g ^{\phi(p)}\equiv 1 \mod p\). Consider \(w^{i}_n = g^{ik}\) for \(0 \leq i < n\), because \(0 \leq ik < nk = p - 1\), by the property of Primitive root modulo n, we can make sure \(\{ w^{0}_n, w^{1}_n, ... , w^{n-1}_n \}\) under modulo \(p\) are unique. (You can prove that \(w^{\frac{n}{2}}_{n} \equiv -1 \mod p\) because \(\{ w^{0}_n, w^{1}_n, ... , w^{n-1}_n \}\) are unique. Therefore, every time you squre \(\{ w^{0}_n, w^{1}_n, ... , w^{n-1}_n \}\), the size of this set will be divided by 2)
Note: If \(w_n \equiv g^k \mod p\), then \(w_{\frac{n}{2}} \equiv g^{2k} \mod p\) because \(p = k \cdot n + 1 = 2k \cdot \frac{n}{2} + 1\).
How to handle inverse of a finite field number
The last missing part is: how can we efficiently compute \(w_n^{-1}\) (that is, the inverse of \(g^k \mod p\))? In fact, we can use Extended Euclidean algorithm. Remember you can compute the \(gcd(a, b)\) by
\[r_{k-2} = q_k r_{k-1} + r_k\]with initial value \(r_{-2} = a\) and \(r_{-1} = b\) (from Wikipedia).
Let us first see why we can definitely find the inverse of a number. Assume \(gcd(a, b) = 1\), by Bezout’s identity, we are guaranteed to find integers \(x, y\), such that:
\[ax + by = gcd(a, b) = 1 \Rightarrow ax \equiv 1 \mod y\]Therefore, if we can calculate \(x\), it will be the multiplicative inverse of \(a\). In our case, \(a\) is \(g^k \mod p\) and \(b\) is \(p\) (which are coprime: \(gcd(g^k \mod p, p) = 1\).
Extended Euclidean algorithm
(Mainly copied from Wikipedia, but add some comments of myself)
As the name shows, this is an extension of your high school Euclidean algorithm:
\[r_{k-2} = q_k r_{k-1} + r_k, s_k = s_{k-2} - q_{k} s_{k-1}, t_k = t_{k-2} - q_k t_{k-1} \text{ (in k's step)}\]with \(s_{-2} = 1, s_{-1} = 0, t_{-2} = 0, t_{-1} = 1\), terminate at \(N\) step when \(r_{N+1} = 0\), then \(s = s_{N}\), \(t = t_{N}\) will satisfy \(s a + t b = gcd(a, b)\).
Proof: We claim that for each \(j\) step,
\[r_j = s_j a + t_j b\]Base case: \(j == 0\)
\[s_0 = 1 - q_0 \cdot 0 = 1, t_0 = 0 - q_0 \cdot 1 = -q_0\]Therefore,
\[s_0 a + t_0 b = a - q_0 b = r_0 \text{ (by the k == 0 step of Euclid algorithm)}\]Assume \(j \leq k - 1\), our claim is correct.
Induction step: by \(k\)’s step of Euclid algorithm:
\[\begin{align*} r_k &= r_{k-2} - q_k r_{k-1} \\ &= s_{k-2} a + r_{k-2} b - q_k (s_{k-1} a + r_{k-1} b) \\ &= (s_{k-2} - q_k s_{k-1}) a + (r_{k-2} - q_k r_{k-1}) b \\ &= s_k a + t_k b \end{align*}\]Thus, at the \(N\)’s step (where \(r_{N+1} = 0\)), we will get
\[s_N a + t_N b = r_N = gcd(a, b)\]by the original definition of Euclid algorithm and our claim above.
Alternative way to compute multiplicative inverse
In our case, our goal is to compute:
\[ax \equiv 1 \mod p\]By Euler’s theorem,
\[a^{\phi(p)} \equiv 1 \mod p \Rightarrow a^{p-1} \equiv 1 \mod p \Rightarrow a^{-1} \equiv a^{p-2} \mod p\]Nevertheless, in practice, we can just swap the result, because if the input polynomial is \(A\) and:
\[(A(w^0_n), A(w^1_n), A(w^2_n), A(w^3_n), A(w^4_n), ..., A(w^{n-1}_n))\]Our goal is to get (By the definition of inverse FFT):
\[\frac{1}{n}(A(w^{-0}_n), A(w^{-1}_n), A(w^{-2}_n), A(w^{-3}_n), A(w^{-4}_n), ..., A(w^{-(n-1)}_n))\]Recall that:
\[w_{n} = g^k \mod p\]Observe that:
\[\begin{align*} w^{n-i}_n &= g^{k (n - i)} \mod p\\ &= g^{kn - ki} \mod p \\ &= 1 \cdot g^{-ki} \mod p \\ &= w^{-i}_n \mod p \text{ (By definition)} \end{align*}\]Therefore,
\[\frac{1}{n}(A(w^{-0}_n), A(w^{-1}_n), A(w^{-2}_n), A(w^{-3}_n), A(w^{-4}_n), ..., A(w^{-(n-1)}_n)) = \\ \frac{1}{n}(A(w^{0}_n), A(w^{n-1}_n), A(w^{n-2}_n), A(w^{n-3}_n), A(w^{n-4}_n), ..., A(w^{1}_n))\], which can be implemented by std::swap efficiently! (and no need to explicitly compute \(w^{-i}_n\))
How to handle negative number
(Thanks to yao11617’s contribution!) In NTT, we are actually perform addition, subtraction and multiplication over \(GF(p)\) (a Finitie Field, where \(p\) is a prime number). We can leverage the idea of 2’s complement. That is, we can represent the numbeer larger than \(\frac{p-1}{2}\) as negative number.
Precisely, \(F = \{0 == 0, 1 == 1, 2 == 2, ..., \frac{p-1}{2} == \frac{p-1}{2}, -\frac{p-1}{2} == \frac{p-1}{2} + 1, .... -1 == p-1\}\)
Let us use several examples to make sure our idea is feasible:
- \[2(2) + (p - 1)(-1) \equiv 1 \mod p\]
- \[3(3) * (p - 7)(-7) \equiv p - 21 \mod p\]
- \[8(8) - (p- 10)(-10) \equiv 18 \mod p\]
Practically, you can map a negative number \(a\) to \(p + a\) and then restore it after performing NTT by \(a - p\) (if the output coefficient is \(a\))!
Isn’t it interesting?
Practical Suggestion
- You can find the useful primitive root of unity table in FFT用到的各種素數 In case of that website crash, I backup that table here:
| \(p = r \cdot 2^{k} + 1\) (prime number) | \(r\) | \(k\) | \(g\) (primitive root) |
|---|---|---|---|
| 3 | 1 | 1 | 2 |
| 5 | 1 | 2 | 2 |
| 17 | 1 | 4 | 3 |
| 97 | 3 | 5 | 5 |
| 193 | 3 | 6 | 5 |
| 257 | 1 | 8 | 3 |
| 7681 | 15 | 9 | 17 |
| 12289 | 3 | 12 | 11 |
| 40961 | 5 | 13 | 3 |
| 65537 | 1 | 16 | 3 |
| 786433 | 3 | 18 | 10 |
| 5767169 | 11 | 19 | 3 |
| 7340033 | 7 | 20 | 3 |
| 23068673 | 11 | 21 | 3 |
| 104857601 | 25 | 22 | 3 |
| 167772161 | 5 | 25 | 3 |
| 469762049 | 7 | 26 | 3 |
| 998244353 | 119 | 23 | 3 |
| 1004535809 | 479 | 21 | 3 |
| 2013265921 | 15 | 27 | 31 |
| 2281701377 | 17 | 27 | 3 |
| 3221225473 | 3 | 30 | 5 |
| 75161927681 | 35 | 31 | 3 |
| 77309411329 | 9 | 33 | 7 |
| 206158430209 | 3 | 36 | 22 |
| 2061584302081 | 15 | 37 | 7 |
| 2748779069441 | 5 | 39 | 3 |
| 6597069766657 | 3 | 41 | 5 |
| 39582418599937 | 9 | 42 | 5 |
| 79164837199873 | 9 | 43 | 5 |
| 263882790666241 | 15 | 44 | 7 |
| 1231453023109121 | 35 | 45 | 3 |
| 1337006139375617 | 19 | 46 | 3 |
| 3799912185593857 | 27 | 47 | 5 |
| 4222124650659841 | 15 | 48 | 19 |
| 7881299347898369 | 7 | 50 | 6 |
| 31525197391593473 | 7 | 52 | 3 |
| 180143985094819841 | 5 | 55 | 6 |
| 1945555039024054273 | 27 | 56 | 5 |
| 4179340454199820289 | 29 | 57 | 3 |
My C++ code
Epilogue
I finally solve https://codeforces.com/problemset/problem/1257/G in 2019/12/27!
(This is also the first time I solve a problem less than 300 people having solved!)
See my code here: main.cc
References
- http://blog.miskcoo.com/2015/04/polynomial-multiplication-and-fast-fourier-transform
- MIT 3. Divide & Conquer: FFT
- Number Theoretic Transform
- Primitive root modulo n
- https://www.wikiwand.com/en/Discrete_Fourier_transform_(general)#/Number-theoretic_transform
- https://www.nayuki.io/page/number-theoretic-transform-integer-dft
- Codeforces tutorial
- Finite Field Made Easy
- The Fast Fourier Transform in a Finite Field